분석 목적
금속 성분 함유량 데이터(변수 1개) - 제품에 금속 재질 함유량의 분산이 1.3을 넘으면 불량이라고 보고 있는데 제조사별로 차이가 난다고 제보를 받았으며 분산에 대한 검정을 수행하기 위함. (유의확률 0.05)
분석 방법
카이제곱 통계량 활용한 단일 표본 분산검정
대립가설: 제품의 금속 재질 함유량의 분산이 1.3을 초과한다.(제품이 불량이다.)
귀무가설: 제품의 금속 재질 함유량의 분산이 1.3 이하이다.(제품이 불량이 아니다.)
양측 검정을 시행하며 분산이 1.3보다 작거나 또는 1.3보다 초과해도 귀무가설을 기각함.
데이터

데이터는 각 제품의 금속 재질 함유량을 나타냄
단일 표본 분산검정
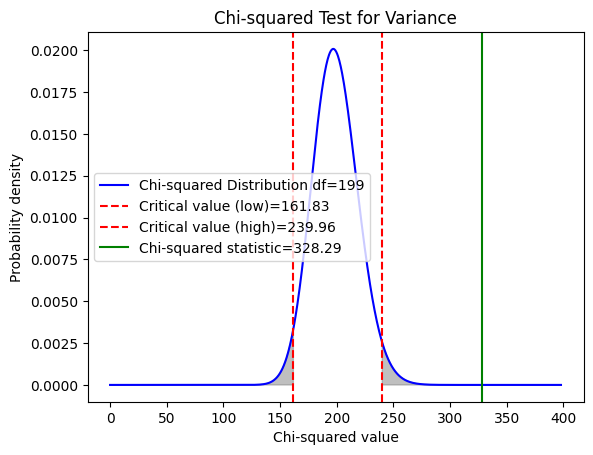
- 샘플 분산: 2.1446
- 카이제곱 통계량: 328.2923
- 임계값(low): 161.8262
- 임계값(high): 239.9597
- p-value: 0

카이제곱 통계량
- N: 표본의 크기
- S^2: 표본 분산
- σ0^2: 귀무 가설 분산
단일 표본 분산분석의 카이제곱 통계량은 표본 분산과 귀무 가설의 분산 사이의 차이가 클수록 값이 커집니다. 즉, 95% 확률로 표본 분산의 카이제곱 통계량이 161.83에서 239.96 사이에 있어야 하지만, 이 범위를 벗어났다면, 이는 95% 신뢰 수준에서 귀무 가설을 기각하게 됩니다. 즉, 관측된 분산이 귀무 가설 하의 분산(1.3)과 유의미하게 다르다고 판단하며, 이러한 경우, 해당 값이 우연히 발생할 확률이 매우 낮다는 것을 의미합니다.
결론
95%의 신뢰 구간의 임계값은 161.83에서 239.96이며, 카이제곱 통계량은 328.29입니다. p-값은 0.05 이내인 0이므로 귀무가설을 기각하고 대립가설을 채택합니다. 즉, 분산은 1.3이 아니며, 제품이 불량이다.
'ADP' 카테고리의 다른 글
| ADP 24회(독립 T검정) (0) | 2024.05.30 |
|---|---|
| ADP 22회(불량률 관리도) (0) | 2024.05.29 |
| ADP 17회(코로나 위험지수) (1) | 2023.11.20 |
| ADP 17회 (시계열 분석) (0) | 2023.11.18 |