이 글에서는 분류 문제에 자주 사용되는 **로지스틱 회귀 분석(Logistic Regression)**에 대해 이해하기 쉽게 설명합니다. 단순한 수식이 아닌, 왜 사용하는지 그리고 어떻게 작동하는지 중심으로 정리했습니다.
로지스틱 회귀란?
- **출력 변수가 범주형(Binary)**일 때 사용하는 회귀 기법입니다.
예: 성공/실패, 예/아니오, 정상/불량 등 두 가지로 나뉘는 결과 예측 - 단순 선형회귀처럼 출력값을 직접 예측하지 않고, 성공 확률 pp을 예측합니다.p=P(success∣X1,X2,...,Xk)
- 즉, 다수의 입력 변수 X1∼Xk로부터 성공 확률을 예측하는 모델입니다.
왜 일반 선형 회귀는 안될까?
선형 회귀를 그대로 적용하면 다음과 같은 형태가 됩니다.
p(X)=β0+β1X1+⋯+βkXk+ϵ
하지만 이 식은 출력값이 -무한대 ~ +무한대까지 나올 수 있습니다.
→ 확률은 반드시 0 ~ 1 사이여야 하므로 부적절합니다.
그래서 나온 해결책: 로지스틱 함수(Logistic Function)
확률값을 선형식으로 예측하기 위해 확률을 **로그 오즈(Log Odds)**로 변환합니다.
logit = ln(p(X)1−p(X)) = β0+β1X1+⋯+βkXk
- **오즈(odds)**는 도박에서 유래한 개념으로, 성공/실패 비율을 의미합니다.
- logit 함수를 통해 좌변도 -무한대~+무한대가 되므로 선형식으로 예측 가능!
최종 식: 로지스틱 함수
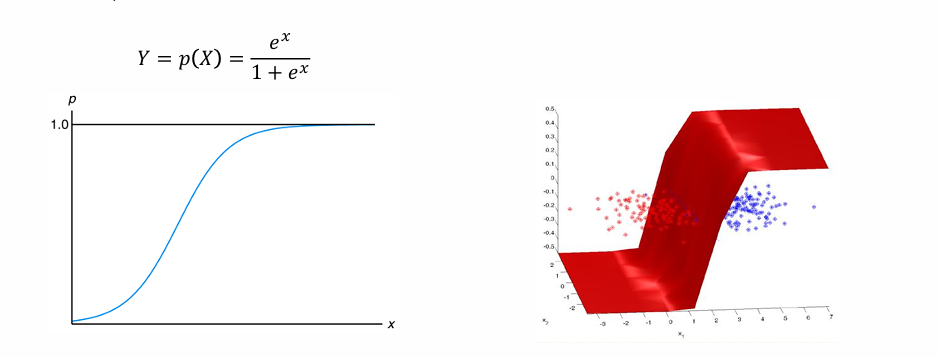
p(X)=1 / { 1+e−(β0+β1X1+⋯+βkXk) }
- S자 형태의 시그모이드 곡선을 따릅니다.
- 출력값은 항상 0 ~ 1 사이 → 확률로 해석 가능
시각적으로 보면?

로지스틱 회귀 예시

- 반도체 공정에서 Pressure 값에 따라 불량 여부(0:정상, 1:불량)를 예측
- 로지스틱 회귀를 사용하면 불량이 될 확률을 예측할 수 있습니다
- 예: Pressure가 2000일 때 불량 확률이 0.5 → 기준값으로 설정
요약

'ML Insights > Regression Analysis' 카테고리의 다른 글
| Ridge 회귀: 다중공선성을 해결하는 정규화 회귀 (0) | 2025.03.26 |
|---|---|
| 회귀계수 축소법: 모델의 성능과 해석력을 높이는 방법 (0) | 2025.03.26 |
| 랜덤포레스트 회귀는 "회귀" 모델일까? (0) | 2025.03.26 |
| 다항 회귀분석 (0) | 2025.03.26 |
| 다중회귀의 진단 (0) | 2025.03.26 |