대선이나 여론조사를 보면, 기관마다 발표하는 결과가 조금씩 다릅니다. 같은 모집단에서 조사를 했는데 왜 다른 결과가 나오는 걸까요? 🤔 이번 포스트에서는 표본 추출의 차이와 신뢰구간의 역할을 중심으로 이를 이해해보겠습니다.
모집단과 표본: 모든 사람을 조사할 수 없을까?
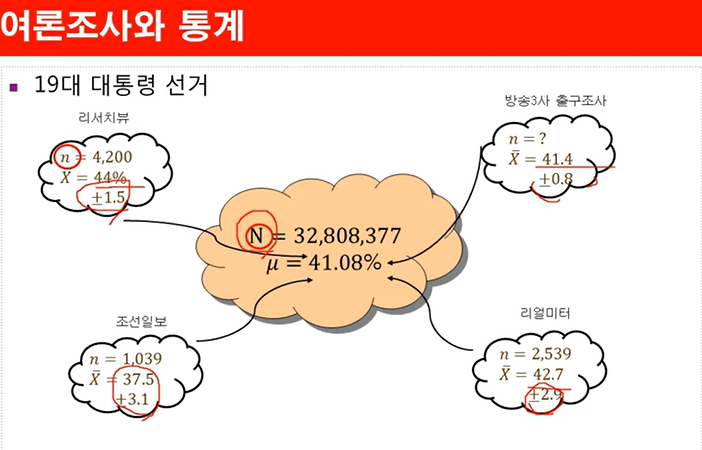
위 이미지에서 보면 **총 유권자 수(모집단, N)**는 32,808,377명, 즉 3천 2백만 명 이상의 유권자가 존재합니다. 하지만, 모든 유권자를 대상으로 조사하는 것은 시간과 비용이 너무 많이 들기 때문에 각 기관은 일부만 추출하여(표본) 여론조사를 진행합니다.
예제: 각 기관의 표본 크기(n) 비교
- 리서치뷰: 4,200명 (표본 평균 44.0%, 오차 ±1.5)
- 조선일보: 1,039명 (표본 평균 37.5%, 오차 ±3.1)
- 리얼미터: 2,539명 (표본 평균 42.7%, 오차 ±2.7)
- 방송3사 출구조사: 표본 수 미공개 (표본 평균 41.4%, 오차 ±0.8)
📌 결과: 표본 평균(𝑋̄)이 기관마다 다름!
✅ 모집단 전체의 실제 지지율(𝜇) = 41.08%
✅ 하지만 표본마다 결과가 37.5% ~ 44% 사이로 달라짐.
왜 기관마다 결과가 다를까? (표본 오차의 원리)
설문조사 결과가 다르게 나오는 이유는 조사마다 표본이 다르기 때문입니다. 같은 모집단에서 뽑아도, 표본에 따라 결과가 다르게 나올 가능성이 큽니다.
예를 들어,
✔ A 기관은 서울과 20대 비율이 높은 표본을 추출했다면? → 결과가 다를 가능성 UP
✔ B 기관은 농촌과 60대 비율이 높은 표본을 추출했다면? → 또 다른 결과
📌 이처럼 표본을 어떻게 구성하느냐에 따라 결과가 다르게 나올 수밖에 없습니다.
신뢰구간: 결과가 다르지만, 범위 안에 들어온다!
표본 조사에서 나온 𝑋̄ (표본 평균)만 보고 모집단을 확신할 수는 없습니다. 그래서 **신뢰구간(confidence interval, CI)**을 사용합니다. 예를 들어, 리얼미터(𝑛 = 2,539)의 결과를 보겠습니다.
- 평균(𝑋̄) = 42.7%
- 신뢰구간(±2.7) → (40.0% ~ 45.4%)
즉, 진짜 모집단의 평균(41.08%)이 이 범위 안에 있을 확률이 높다! 이것이 신뢰구간의 역할입니다.
🔹 다른 기관들도 신뢰구간을 보면 모집단의 실제 값(41.08%)을 포함하고 있습니다.
🔹 즉, 조사마다 결과가 달라도, 신뢰구간 내에서는 모집단 평균과 일치할 확률이 높다는 뜻!
✅ 결론: "표본은 다르지만, 신뢰구간을 보면 실제 모집단 값을 포함할 가능성이 크다!"
정리 및 결론
📌 여론조사 결과가 기관마다 다른 이유?
✔ 모집단 전체를 조사할 수 없어서 표본을 추출해야 함.
✔ 기관마다 표본 크기(𝑛)와 구성이 다름.
✔ 따라서 𝑋̄ (표본 평균) 값이 다르게 나올 가능성이 높음.
📌 그럼에도 불구하고, 신뢰구간이 중요한 이유?
✔ 표본 평균 자체만 보면 차이가 커 보이지만, 신뢰구간을 보면 모집단의 실제 값(41.08%)을 포함할 확률이 높음.
✔ 즉, 조사마다 값이 다르다고 해서 틀린 조사는 아님!
✔ 중요한 건 신뢰구간 안에 모집단의 실제 값이 포함될 확률이 높다는 것!
📌 마무리: 신뢰구간을 꼭 확인하자!
다음번에 여론조사 결과를 볼 때, 단순히 지지율(𝑋̄) ->점추정만 볼 것이 아니라 ±오차(신뢰구간)까지 확인하면 훨씬 더 정확한 해석이 가능하겠죠? 😊
👉 결과는 달라 보여도, 신뢰구간 안에 포함될 확률이 높다!
👉 여론조사 데이터를 해석할 때는 신뢰구간을 꼭 확인하자!